Inflation is NOT Always and Everywhere a Monetary Phenomenon

Monetarism is a hoary old myth that does its damage in two distinct ways. The first is that, piggybacking on Milton Friedman’s personality, basically an entire generation of economists are actually monetarist in their practical thinking. Greg Mankiw once remarked that New Keynesianism should more accurately be called New Monetarism and a glance at the actual pronouncements of even the more self-critical the New Keynesians shows this beyond a shadow of a doubt.

The second way in which monetarism does its damage is what might be called ‘man-in-the-street-monetarism’. Man-in-the-street-monetarism is the knee-jerk reaction you get from people who have no training in economics (and some people who actually do but obviously weren’t paying close attention!) but who nevertheless read about economic matters and so forth. When they hear ‘money printing’ they instantly think ‘inflation’. This can interfere with conversations at dinner parties but it also infects the journalistic media. In its more extreme forms it leads people into economic cults like the neo-Austrian school that has become so popular on the internet after the financial crisis. These poor suckers are then sold gold and other dodgy investment vehicles by industry frontmen.

The essence of monetarism is in the transformation of an identity put forward in Irving Fisher’s classic 1911 work The Purchasing Power of Money into a supposed causal relationship. In that work Fisher laid out the following identity:

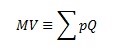That equation reads: “The amount of money, M, multiplied by its velocity, V, is equal by identity to the sum of the quantity of goods and services purchased, Q, times the sum of their prices, p.” Note the clause “equal by identity”. The equals sign with an extra bar indicates that this is a tautological statement. It simply must be true. In the book Fisher discusses a number of ways in which this identity might hold. I think that while Fisher’s discussion was far more nuanced than the monetarists that grew out of the 1960s and 1970s it is nevertheless quite misleading. I lay out this argument in the chapter on money in my forthcoming book.

The monetarists proper converted this identity into a behavioral equation. This equation ran as follows and should be read running from left to right:

Note two things. First, the fact that we have converted the “equal by identity” sign into a standard equals sign. This implies causality running from left to right. So, the left-hand side of the equation causes the right-hand side. Secondly, we have placed ‘hats’ on the velocity and quantity variables. This implies that they are to be thought of as fixed. Thus the equation reads: “The sum of prices is equal to the quantity of money”. We understand the sum of prices here to be the Consumer Price Index (CPI).

Even when Friedman first came out with these statements they were showed to be empirically vacuous in the classic empiricist, anti-monetarist text The Scourge of Monetarism by Nicholas Kaldor. But today we have easy access to these statistics and can quickly run the relevant regressions. So, let’s see how monetarism fairs when confronted with the facts today.

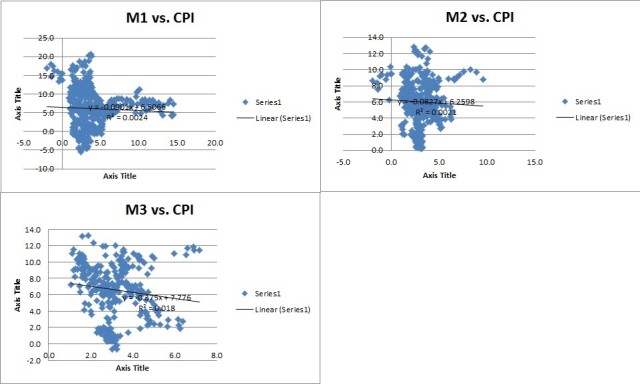
First it should be noted that one peculiar feature of monetarism is its vagueness. When monetarist policies were implemented in the late-1970s and early-1980s and did not have the intended effects, monetarist economists began to cast doubt on the measures being used to calculate the money supply. Any time the policy didn’t work the economists would say that the central banks were not measuring the money supply properly. This is a classic use of theoretical argument to immunise marginalist economic theories against empirical criticism and was a tendency much discussed by the neo-positivist philosopher Hans Albert. For this reason we will include three key measures of the money supply — M1, M2 and M3 — and plot them against the CPI to give the theory the best possible chance to come to empirically verifiable conclusions. All the data that follows comes from FRED and the years chosen are based on availability.

Let us first lay these out in a standard graph form to see if we can intuitively spot any correlation. All graphs measure percentage changes year-on-year of both variables mapped. The reader can click on the image to enlarge it.

Oh dear, oh dear. Typically we should be able to pick up any correlation intuitively but in the above graphs — which represent all the data that FRED provides on the various money supply measures — we really do not see much to be hopeful for. Nevertheless, let us run some simple regressions to see if there is a correlation hiding in plain view that our all-too-human faculties have missed.

Oh no! This is very bad news for our monetarist friends. First of all, we must note that if the monetarist theory is true we should see a positive correlation between the money supply and prices. That is, when the money supply rises so too should prices and vice versa. This would be indicated in the regressions by an upward-sloping trendline. But in all three regressions we see a negative correlation indicated by a downward-sloping trendline. Embarrassing!

Secondly, we should note that the correlation coefficient, annotated the R-squared, is very, very weak in all three regressions. This is reflective of the intuitive fact that the graphs we laid out previously showed no significant relationship between the variables. Thirdly, we should note that the generally favoured measure of the money supply by monetarists is the M3 and in our regressions the M3 had the lowest correlation coefficient and the most substantially negative relationship. If these regressions are anything to go by we should more so expect prices to fall when the M3 grows!

But before we take our leave from monetarist fantasyland let us zoom in on the best ‘natural experiment’ of the thesis that we find in the data: namely, the extreme events surrounding 2008. Here is the data for the M1 and the M2 plotted against the CPI for that era (data for M3 is not available as it was discontinued in 2005):

Again, the data seems to run entirely contrary to the monetarist theory. Recall that above we read the monetarist equation to say that an increase in the money supply causes a rise in prices. But here we see both money supply measures rising toward the end of the 2008 as prices fell. This runs exactly contrary to what the monetarists would have you believe. Indeed, the negative relationship between the M1 monetary base and the price level is extremely statistically significant. Here is a regression plotting that important 12 month period:

All we can conclude from this is that monetarist theory — whether in academic form or in its man-in-the-street variant — is deeply, deeply misleading. The real world facts seem to run exactly contrary to the theory. Indeed, I do not think you could hope for a stronger refutation of any theory by engaging in data analysis. And yet the theory will continue to live on, zombie-like in the minds of academic economists, the media and the general public. Why? Why did this doctrine impose itself on the minds of men, especially in the 1970s and 1980s?

This, I think, is when ideology comes to play a role. I have documented some reasons for the rise of monetarist doctrine in this era on this blog before and readers can consult that particular post. But that post mainly focused on the case of the UK. With regards to the US James Galbraith and William Darity Jr. put forward the following argument as to monetarism’s supposed adoption by the Federal Reserve in the late-1970s and early-1980s in their excellent textbook Macroeconomics:

The Federal Reserve was no more monetarist in the early 1980s than it had ever been; it merely found for a time that monetarist arguments could be used to justify a severe credit crunch, and resulting recession, when these were felt necessary to bring a rapid end to inflation. (p244)

Amen to that!